Equations of State II

Notes following Ch. 3 of Pols Lectures here & HKT, Ch. 3, Available Online.

Day 4 - September, 9, 2025

Agenda:

• Updates/Reminders - HW1 Due Thur. Sept. 18 before class (2m)
• Lecture (25m)
• In-Class Activity 4 - Groups of 2 - Due end of day (30m)
• Report out on ICA in ica Slack Channel (10m)

Recap: Mixture of (non-relativistic, classical) gases

Each gas will contribute to the pressure:

Today, we will talk about additional terms to the total pressure and when quantum mechanic effects might play a role.

Quantum-mechanical effects

Let's relax the hypothesis that the gas behaves classically.

Q: A star is "big", why do we need to care about quantum mechanics?

• QM effects can matter at "low" temperatures and/or "high" densities, which can be encountered in stellar physics.

Sirius A, the Dog Star, and Sirius B
Image Credit & Copyright: NASA, H.E. Bond and E. Nelan

Quantum-mechanical effects

The limit on the precision to which position and velocity of a particle can be known (Heisenberg's uncertainty principle): with Planck's constant. For a three-dimensional volume this becomes

Thus the available number of quantized states is

is the number of intrinsic quantum states of the particle, e.g. spin.

Quantum-mechanical effects

• The key point here is to satisfy QM.

Let's start by considering a classical gas in non-extreme regime. Then
the particles are distributed according to a Maxwell-Boltzmann
distribution , but whenever , we know this is going
to violate QM!

Quantum-mechanical effects

From the previous lecture we have already seen the Maxwell-Boltzmann distribution (Pols 3.13)

Taking the ratio to our equation for we find that

Q: How can we use this to find when QM effects become important?

Quantum-mechanical effects

• at fixed temperature , for very high number densities , this ratio is going to be larger than one in violation of QM
• at fixed number density , for very low temperatures , this ratio will be larger than 1 in violation of QM.
• smaller mass particles will violate QM earlier than the higher mass particles.

Quantum-mechanical effects

We can expect that for "very cold" stars or "very dense" stars the ideal gas EOS will not be appropriate.

• To account for QM effects, we need to consider the nature of the particles making up the star, which can be either Fermions or Bosons.

Image Credit: Hugo Spinelli

Quantum-mechanical effects

• Fermions with semi-integer spin, such as electrons and nucleons (protons or neutrons).

The occupation of quantum states of energy between and is determined by the Fermi-Dirac distribution (Pols 3.26):

where is the "degeneracy parameter" dependent on the chemical potential . Pauli's exclusion principle states each quantized energy state can be occupied by at most one fermion.

Quantum-mechanical effects

• Bosons with integer spin, such as photons, or particles. In this case the relevant distribution is the Bose-Einstein's distribution:

which can be 1, meaning more than one boson can occupy the same energy level (e.g., in the extreme case of a Bose-Einstein condensate all particles occupy the level with lowest - this maybe relevant in the interior structure of neutron stars for example).

Quantum-mechanical effects

The total number of particles with momentum between and is thus given by for an appropriate choice of depending on the particle considered ( or ). To determine the chemical potential one can impose the normalization following from:

that is integrating the phase space distribution in momentum one
should find the spatial density of particles.

Complete electron degeneracy

Let's now consider a gas of electrons. These are the particles in the
ionized gas of the star that will first start feeling QM effects,
since (in fact ).

• These particles have spin 1/2, thus they are fermions, and obey with (each quantum cell of the phase space can be occupied by 2 electrons, one with spin up and one with spin down).

• A fully (completely) degenerate gas is one where all the particles are in the lowest possible energy state, corresponding to the limit .

Complete electron degeneracy

Fermions (such as electrons) occupy a sphere in momentum space with radius called the Fermi momentum:

and we used for electrons. To find the value of we can use
the normalization coming from the total number density of electrons

Complete electron degeneracy

The Fermi momentum depends only on the density of electrons for a fully degenerate electron gas.

We can now calculate the pressure for the gas using our original equation for pressure (Pols 3.4):

We just neet just need the appropriate relaton for the momentum. Lets first consider the non-relatvisitc limit for this gas.

Complete electron degeneracy (Non-relativistic)

In this case is the energy of the electrons (still ideal
gas) and , and from Pols 3.31

where we used Pols Eqn. 3.18 for .

A fully degenerate, non-relativistic electron gas has a polytropic EOS with exponent .

Complete electron degeneracy (Ultra-relativistic)

In the extremely relativistic limit, we can assume (i.e. neglect the rest energy of the electrons in the relation), and then we lose
one power of in the integral below:

A fully degenerate extremely/ultra-relativistic gas, the EOS will again be a polytrope with exponent now .

Complete electron degeneracy (Ultra-relativistic)

In general, we should expect a smooth transition between these two
regimes as increases.

One can estimate the density at the transition with the
condition :

The density around which we expect a transition from non-relativistic to ultra-relativistic gas only depends on and fundamental constants!

Partial degeneracy

The equations derived above are valid in the strict limit of ,
necessary for full degeneracy.

In reality it is sufficient to have where (which defines what is "cold" enough to get QM effects on the pressure contribution for non-relativistic electrons). This is equivalent to asking with electron degeneracy parameter.

Summary on Electron Degenerate Gas

• Electrons are Fermions that need to obey Pauli's principle at very low (comparing their kinetic energy to the Fermi energy) and/or very high

• they can exert a much larger pressure than predicted by the classical ideal gas.

• The pressure is a polytrope, independent of temperature T! Exponent depending on if the gas is NR/ER.

This is the situation of a "white dwarf" (WD, such as Sirius B), which are the remnants for the vast majority of stars, including the Sun.

Radiation pressure

In some stars, the radiation field is so strong that is has a non-negligible contribution to the pressure.

• The particles providing that pressure are photons, which are bosons with 2 possible polarization states, so .

We use this to determine the number density:

Radiation pressure

and the energy density due to radiation

where

which is closely related to the Stefan-Boltzmann constant : .

Radiation pressure

Relying again on the ultra-relativistic nature of photons, we know
that (Pols 3.12) and therefore the radiation pressure is:

• Q: So far we have assumed full ionization of the gas. What do you think may change if we account for partial ionization? And where may that be important?

Pressure of a mixture of gas and radiation

Putting all things together:

If the electrons are not degenerate (they can be described classically as in Pols 3.19),

In practice, stellar evolution code often rely on tabulated EOS, which account for many non-ideal effects.

Pressure of a mixture of gas and radiation

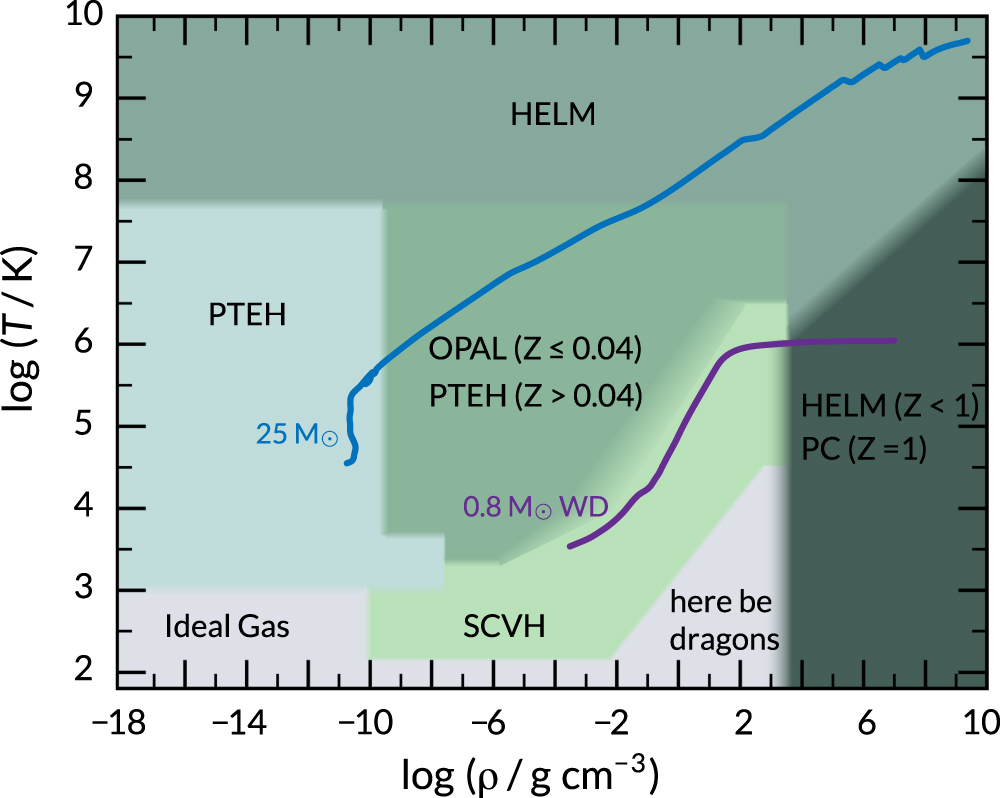
EOS are ultimately one of the points of contact between stellar physics and atomic physics and statistical mechanics:

The ρ–T coverage of the EOS used by the eos module. From the MESA V instrument paper by Paxton et al. 2019.

Note: these are profiles, not history data.

In-Class Assignment 4

In class: Work on ICA here with partner, I will ask one or two people to share and describe plots at the end of class.

After Class: End of day today, September, 9, 2025

• Submit as a PDF, preferrably using nbconvert to D2L, the progress you have made.

ICAs are not always designged to be completed but rather worked on in class, submit what you have when you leave the class even if you did not make much progress.