Heat Transfer by Convection

Notes based on Sec 5.5 in Onno Pol’s online lecture notes here and HKT Chapter 5.

Wednesday, Feb. 12, 2025

astrophysics of stars and planets - spring 2025 - university of arizona, steward observatory

Today’s Agenda

1. Announcements (2m)

2. Reading Overview/Key Points (10m)

3. In-Class Activity 10 (20m)

4. Debrief/Reminders (2m)

Criteria for stability against convection

Similar to heat transport via radiation, we require a temperature gradient. However, there is a limit to the possible temperature gradient that would be required for some luminosity values. If this limit is exceed then an instability sets in, leading cyclic macroscopic motions of the gas, known as convection.

Schematic Diagram of Convection

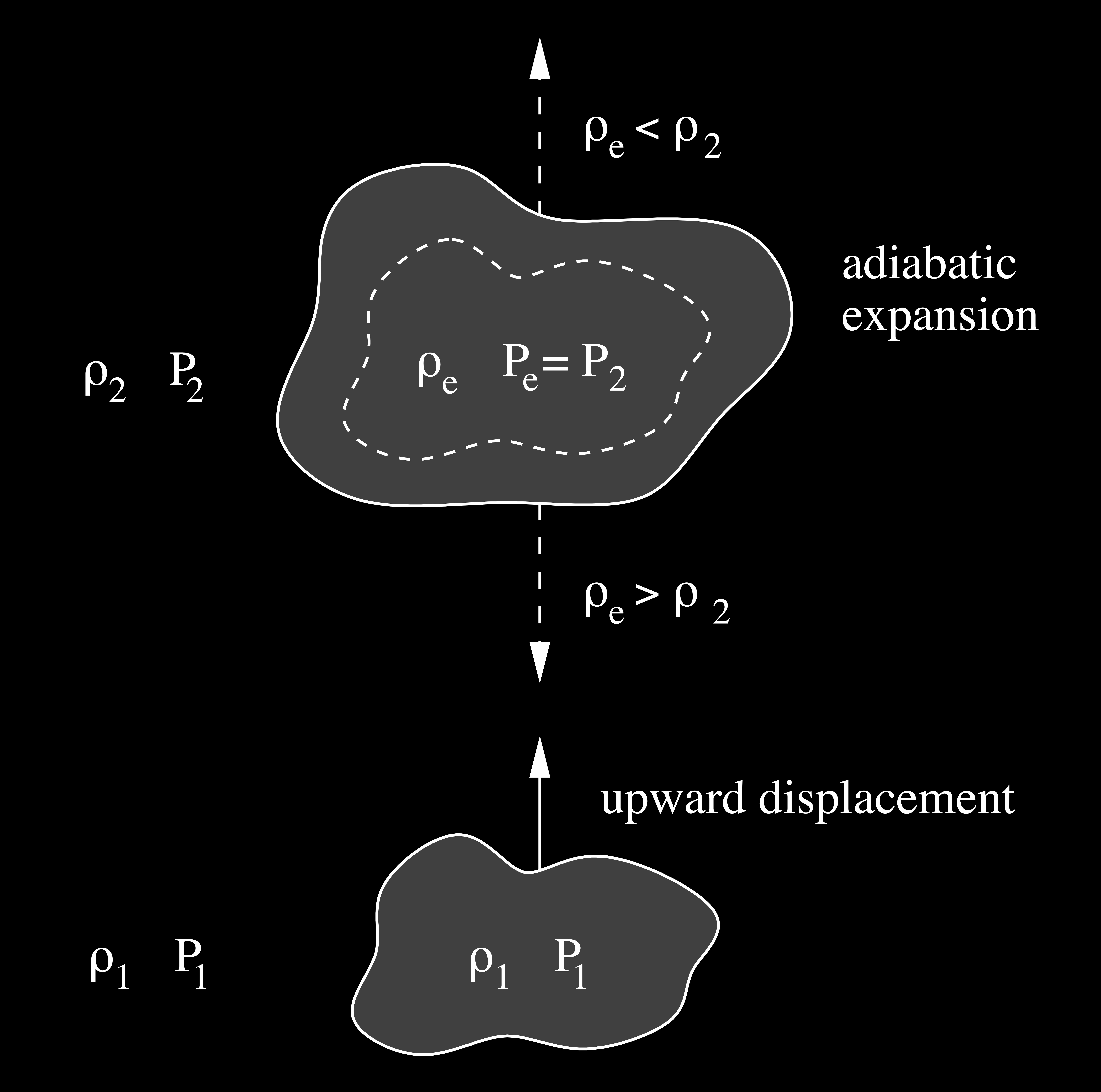
Credit: Onno Pols - Stellar Structure and Evolution - Schematic illustration of the Schwarzschild criterion for stability against convection.

1. A gas element is perturbed and displaced upwards from position 1 to position 2,

2. the blob expands adiabatically (no heat exchange \(\textrm{d}q=0\)) to maintain pressure equilibrium with its surroundings. \(P_{2}=P_{\rm{equilibrium}}\).

If \(\rho_{2} > \rho_{\rm{equilibrium}}\) - the blob will sink back down to position 1.

If \(\rho_{2} < \rho_{\rm{equilibrium}}\) - buoyancy forces will accelerate it upwards, convection occurs.

This expansion of the blob over \(\Delta r\) takes place on the local dynamical timescale (i.e. with the speed of sound).

Schwarzschild Criterion

The simplest form of criteron for stability against convection is known as the Schwarzschild Criterion:

Definition 81

\[ \nabla \lt \nabla_{\rm{ad}} \]

In words, a region is considered to be stable against convection (non-convective) if the actual temperature gradient (recall \(\nabla_{\rm{actual}} = \textrm{d \ log} T / \textrm{d \ log} P\)) is less than the adiabatic temperature gradient.

If all of the energy is presently transported by radiation then we can replace \(\nabla\) with \(\nabla_{\rm{rad}}\) to arrive at:

Definition 82

\[ \nabla_{\rm{rad}} \lt \nabla_{\rm{ad}} \]

However, this criterion assumes a chemically homogeneous star. We could, instead, have changes in the mean molecular weight \(\mu\).

Ledoux Criterion

Consider a change in the mean molecular weight \(\mu\), with a non-zero (\(\nabla_{\rm{\mu}}= \textrm{d log} \mu / \textrm{d log} P\)). This leads us to what is know as the Ledoux criterion for convection. A region is stable against convection if the following is true

Definition 83

\[ \nabla \lt \nabla_{\rm{ad}} - \frac{\chi_{\mu}}{\chi_{T}} \nabla_{\mu} \]

where \(\chi_{\mu}\equiv \left ( \textrm{d log} P / \textrm{d log} \mu \right )_{\rho,T}\). Because \(\mu\) normally increases inward, \(\nabla_{\rm{\mu}}\geq0\), the result is that \(\mu\) gradients can lead to a stabilizing effect.

For convection to occur, you typically will need one of the following:

1. a large \(\kappa\), convection occurs in opaque regions of a star.

2. region with large energy flux, stars with \(\epsilon_{\rm{nuc}}\) values near the center are expected to have convective cores - massive stars.

3. a small value of \(\nabla_{\rm{ad}}\) such as at partial ionization zones at relatively low temperatures. stars of all masses have shallow surface convection zones at temperatures where hydrogen and helium are partially ionized.

The Mixing Length Theory

Stellar fluid comprised of parcels, eddies, elements, bubbles, or blobs that can move from regions of high heat to regions of lower heat content. These blobs are capable of transporting or convecting heat through the fluid. MLT is a local theory.

Assumptions in the MLT

1. A readily identifiable parcel has a characteristic dimension of the same order of size as the mixing length \(\ell\).

2. The mixing length is much shorter than any scale length associated with the structure of the star – such as the pressure scale height, \(H_{\rm{P}}\) or \(\lambda_{\rm{P}}\). In practice, \(\ell \sim H_{\rm{P}}\).

3. The parcel always has the same internal pressure as that of its surroundings.

4. Acoustic phenomena may be ignored altogether, as may shocks, etc.

5. Temperatures and densities within and outside a parcel differ by only a small amount

Within the MLT framework we can compute some relevant properties including:

the average convective velocity (\(v_{\rm{conv.}}\))

Definition 84

\[ v_{\rm{conv.}} \approx \sqrt{1/2 \ell g \frac{\Delta T}{T}} \approx \sqrt{\frac{\ell^{2}g}{2H_{\rm{P}}} (\nabla - \nabla_{\rm{ad}})} \]

and the convective energy flux (\(F_{\rm{conv.}}\)) compare with HKT 5.38

Definition 85

\[ F_{\rm{conv.}} = \rho c_{\rm{P}} T \left ( \frac{\ell}{H_{\rm{P}}} \right )^{2} \sqrt{1/2 g H} (\nabla - \nabla_{\rm{ad}})^{3/2} \]

where the term \(\nabla-\nabla_{\rm{ad}}\) is referred to as the superadiabicity.

Convective Mixing

Convection is also an efficient mixing mechanism. For the Sun, we can estimate convective velocity speeds of \(v_{\rm{conv.}}\approx5\times10^{3} \ (\textrm{cm s}^{-1})\). These speeds are enough to mix on an efficient timescale, \(\tau_{\rm{mix}}\approx d/v_{\rm{conv.}}\) leading to mixing timescales of weeks to months, \(\tau_{\rm{mix}} \ll \tau_{\rm{KH}} \ll \tau_{\rm{nuc}}\).

This leads to the following consequences in general for stellar structure, the large efficiency of convective mixing means:

1. A star in which nuclear burning occurs in a convective core will homogenize the region inside the core

2. A star with a deep convective envelope, such that it extends into regions where nuclear burning has taken place, will mix the burning products outwards towards the surface. This processed is called the dredge-up.

Convective Overshoot

When a convective blob crosses the boundary of the convective region, it will have a non-zero velocity. On average, some blobs will overshoot this boundary and extend beyond the boundary defined by the criterion.

Often this is parameterized in stellar evolution calculations, where \(d_{\rm{ov}} = \alpha_{\rm{ov}}H_{\rm{P}}\) a fractional distance of the local pressure scale height averages the blobs that overshoot the classical convective boundary.

\(\rm{Brunt-V\ddot{a}is\ddot{a}l\ddot{a}} \ frequency\)

Another means of determining if a region is convectively stable is the \(\rm{Brunt-V\ddot{a}is\ddot{a}l\ddot{a}} \ frequency\) defined as (HKT 5.29/9.11):

Definition 86

\[ N^{2} = g \left [ \frac{1}{\Gamma_{1} P} \frac{d P}{dr} - \frac{1}{\rho} \frac{d \rho}{dr} \right ] \equiv -\frac{\chi_{T}}{\chi_{\rho}} (\nabla - \nabla_{\rm{ad}}) \frac{g}{H_{\rm{P}}} \]

in convective regions, \(N^2<0\).

Hydrodynamic Calculations

Computational modeling of stellar hydrodynamics have advanced our understaning of stellar structure and evolution.

We can use multi-dimensional stellar modeling to constrain free parameters in MLT and other mixing processes such as convective overshoot, calibration of the mixing length free parameter, convective velocity speeds, 3D velocity distrubutions.

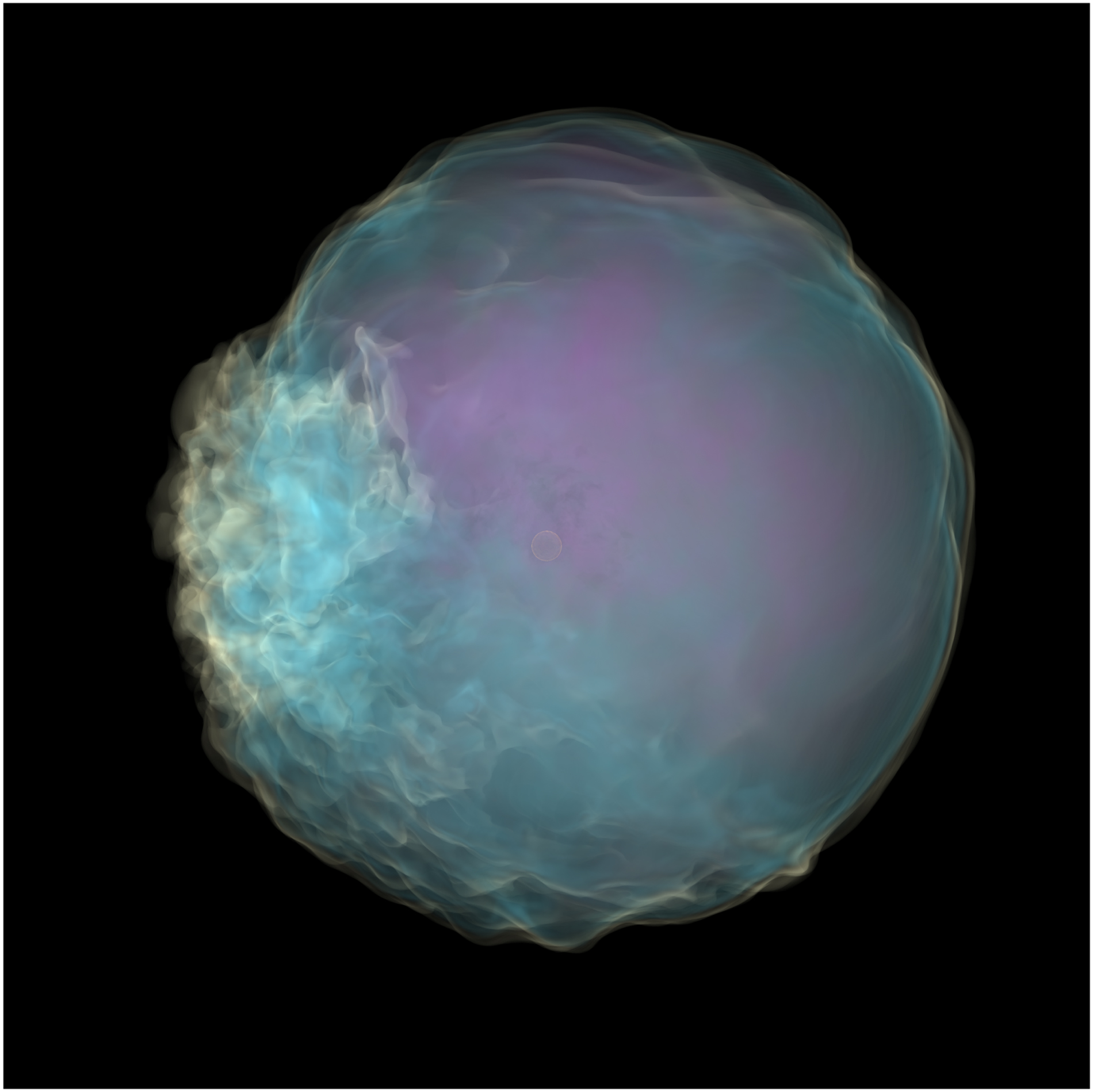
Here I show an example of stellar convection in the O-shell burning region in a \(20 M_{\odot}\) near iron core-collapse from C. E. Fields and Sean M. Couch 2021 ApJ 921 28. In this work, we find that convective velocities are on average 2-3 times that of those predicted by MLT.

In-Class Assignment

In-Class Assignment 10 is here.