The Sun

Friday, Feb. 28, 2025

astrophysics of stars and planets - spring 2025 - university of arizona, steward observatory

Notes based on HKT 9.1-9.3.

Today’s Agenda

1. Announcements - Midterm Review Available on D2L (2m)

2. Reading Overview/Key Points (10m)

3. Catch up - help with HW3, start midterm review/assign problems, leave early (25m)

The Present-Day Sun

Composition

Most values are from Asplund et al 2009 - The Chemical Composition of the Sun. A09 in MESA.

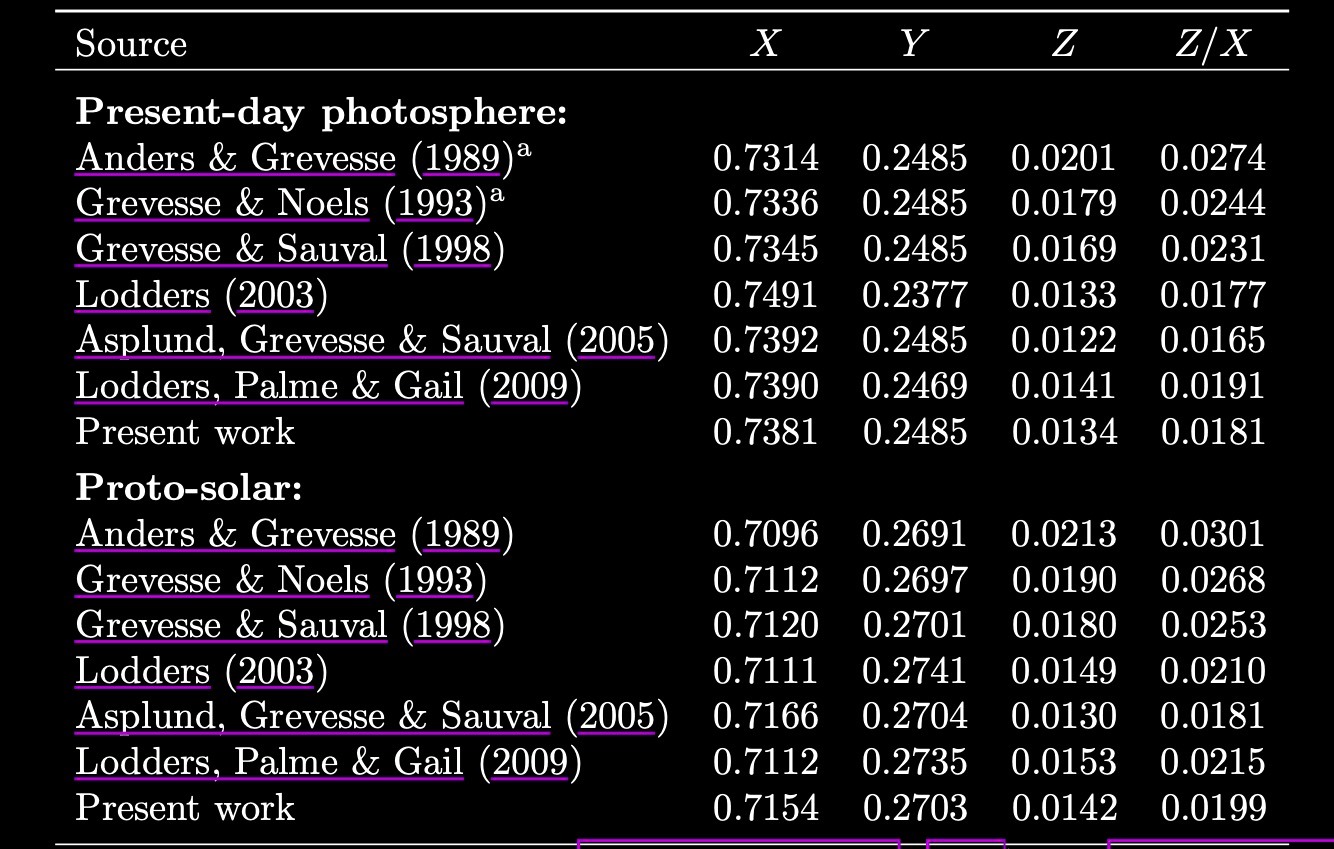
The mass fractions of hydrogen (\(X\)), helium (\(Y\)) and metals (\(Z\)) for a number of widely-used compilations of the solar chemical composition. Credit: Asplund et al 2009.

Combination of observed signatures, atmosphere modeling, and direct measurements from meteorites.

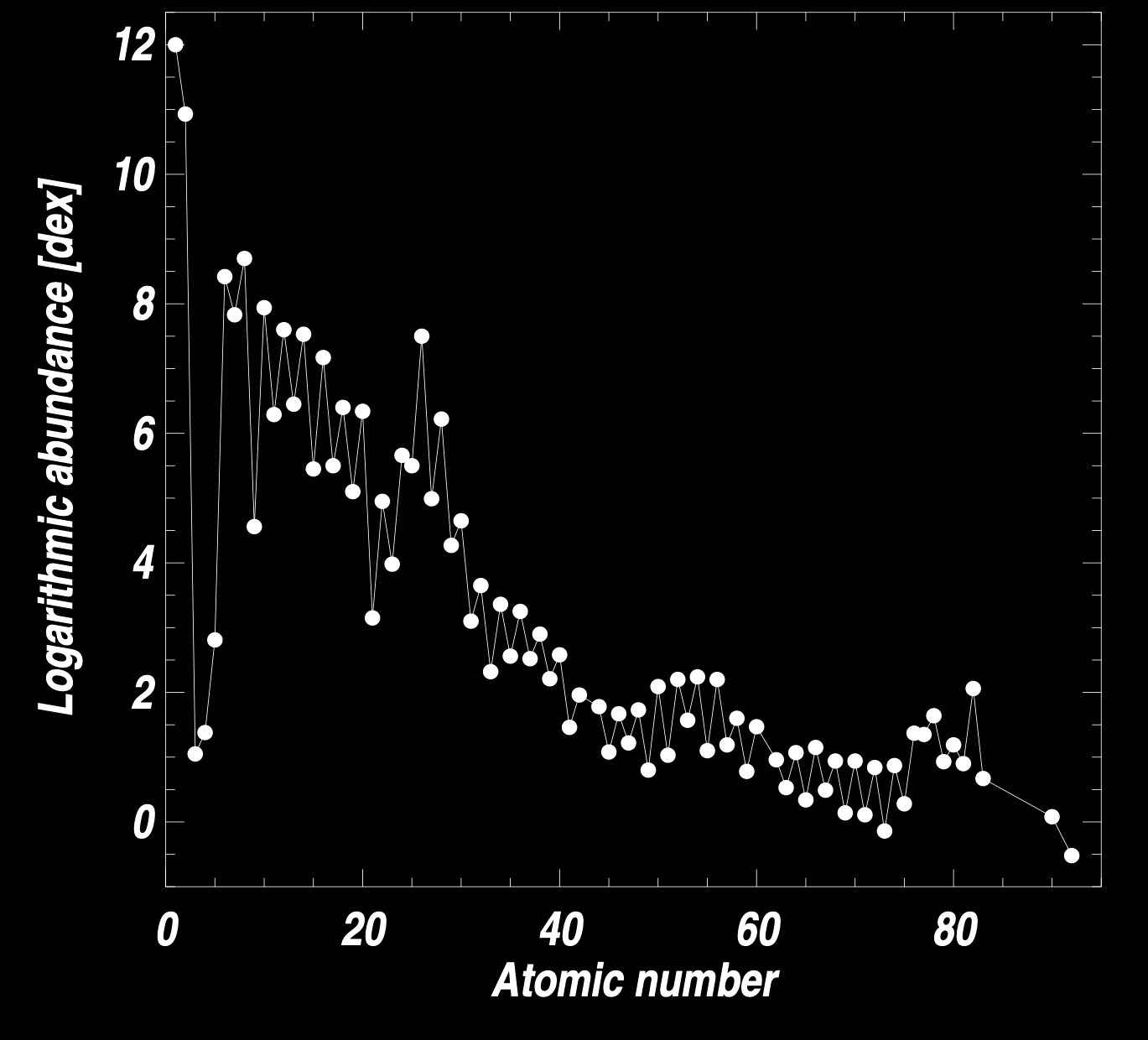
The present-day solar photospheric elemental abundances as a function of atomic number.

Here, we have adopted the logarithmic abundance scale

\[ \textrm{log} \epsilon_{H} = 12.00 \]

and

\[ \textrm{log} \epsilon_{X} = \textup{log}(N_{X}/N_{H}) + 12.00 \]

that is, everything is scaled relative to Hydrogen. Here, dex is for decimal exponent.

Structure

Some definitions:

The local adiabatic sound speed:

Definition 110

\[ v^{2}_{\rm{s}} \equiv c^{2}_{\rm{s}} = \left ( \frac{dP}{d\rho} \right )_{\rm{ad}} = \Gamma_1 \frac{P}{\rho} \]

The \(\rm{Brunt-V\ddot{a}is\ddot{a}l\ddot{a}}\) Frequency (N):

Definition 111

\[ N^{2} = g \left [ \frac{1}{\Gamma_{1}P} \frac{dP}{dr} - \frac{1}{\rho}\frac{d \rho}{dr} \right ] \equiv - \frac{\chi_{T}}{\chi_{\rho}} (\nabla - \nabla_{\rm{ad}}) \frac{g}{\lambda_{\rm{P}}} \]

in convective zones when \(\nabla\gt\nabla_{\rm{ad}}\), \(N^{2}<0\).

the frequency of oscillation associated with a perturbed parcel of fluid in a convectively stable medium for \(N^2\gt0\).

The Lamb frequency:

Definition 112

\[ S^{2}_{\ell} = \frac{\ell(\ell+1)}{r^2}\frac{\Gamma_1 P}{\rho} \equiv \frac{\ell(\ell+1)}{r^2}v^{2}_{s} \]

Observation of p-modes allow us to infer the sound speed in the Sun!

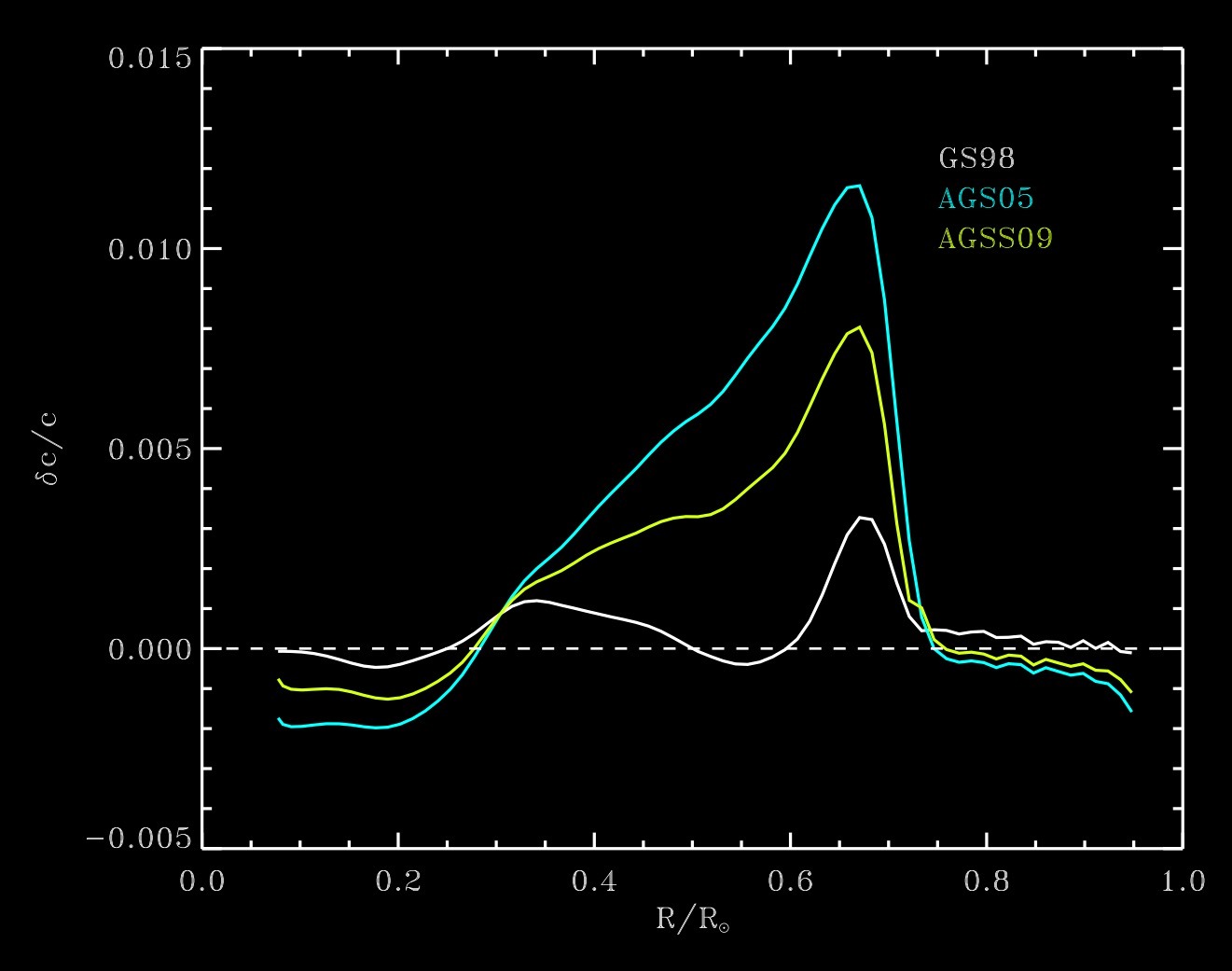
The differences between the helioseismic and predicted sound speeds as a function of depth (Serenelli et al. 2009). Credit: Asplund et al 2009.

More details on deriving the profile from helioseismology are discussed in Basu et al 2009.

Observation 12

The largest discrpencies are at the base of the convection zone, the tacholine region, and is affected by the differential rotation of the sun in the convective region.

The Solar Neutrino “Problem”

A “problem” in matching the observed neutrino rate from the Sun and the predicted rate from standard model for neutrino flux.

First example by the Homestake Mine experiment which established a measured value of \(2.56\pm0.23\) SNU (“snoo”, \(10^{-36}\) captures s\(^{-1}\) target\(^{-1}\)).

The predicted flux for the experiment was \(7.6\pm1.2\) SNU!

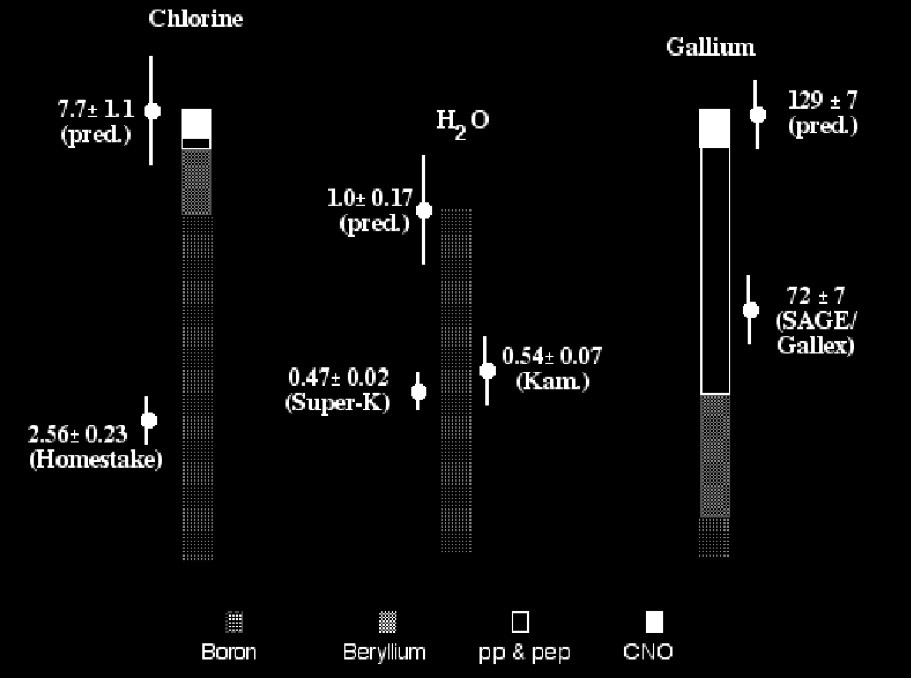
The solution was neutrino oscillations! Neutrinos can change “flavor” as they travel: electron, muon, or tau.

1. The Homestake experiment could only detect electron neutrinos - 1/3.

2. Super-K mostly sensitive to electron, can also detect some muon and tau - though cannot distinguish - closer to expected rate.