Rotation

Rotation#

Additional Recommended Resource: Physics, Formation and Evolution of Rotating Stars by André Maeder.

Friday, Mar. 21, 2025

astrophysics of stars and planets - spring 2025 - university of arizona, steward observatory

Today’s Agenda#

  1. Announcements - HW3 Corrections due EoD (2m)

  2. Reading Overview/Key Points (5m)

  3. ICA 15 - Gravity Darkening in Low Mass Stars (25m)

  4. Debrief + Share Results (5m)

von Zeipel’s Paradox#

\[ \large \textrm{A uniformly rotating star cannot be in steady-state radiative thermal equilibrium. Something must give.} \]

Let’s start to show this by assuming a cylindrical coordinate system: \(\textbf{r}=\textbf{r}(\bar{\omega},\phi,z)\)

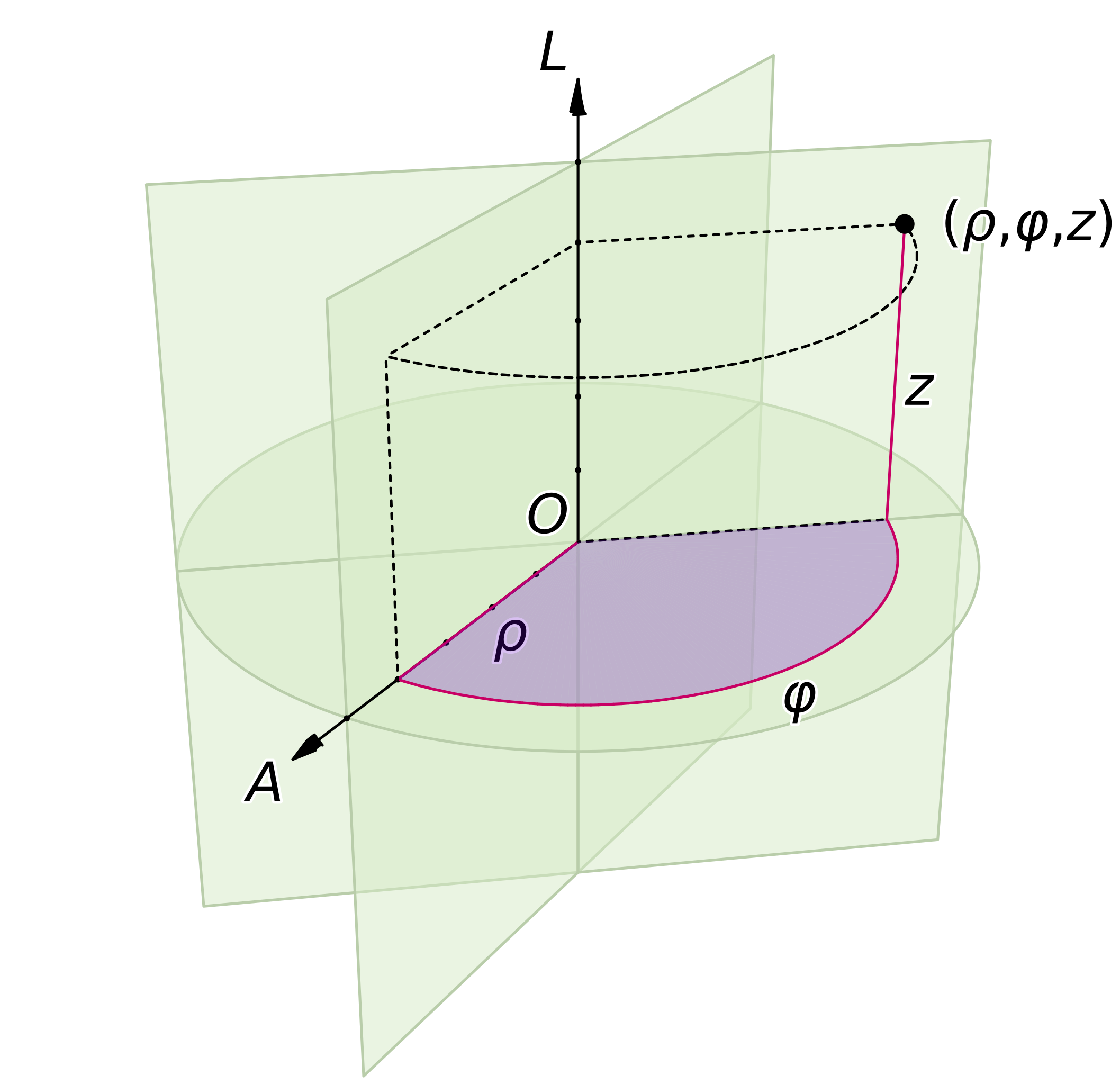
../../_images/cyl.png

  • \(z\) is aligned with the axis of rotation, “rotation about the Z-axis”

  • \(\bar{\omega}\) is measured from the z-axis.

We wish to modify the equation of HSE to include the effects of centrifugal force (the apparent outward force on a mass when it is rotated). HSE is our first constraint for such a model.

The first step is to create the total gravitational (or effective potential),

Definition 113

\[ \Phi_{\rm{eff}}(\bar{\omega},z) = \Phi_{\rm{grav}}(\bar{\omega},z) - \frac{\Omega^2 \bar{\omega}^2}{2} \]

where \(\Phi_{\rm{cent}}=-\Omega^2 \bar{\omega}^2/2\) and \(\Omega\) here corresponds to the angular rotation frequency (rad/s).

This leads to our HSE equation now of the form:

Definition 114

\[ \frac{1}{\rho} \nabla P = - \nabla \Phi_{\rm{eff}} = - \nabla \Phi_{\rm{grav}} + \Omega^2 \bar{\omega}^2 \textbf{e}_{\bar{\omega}} \equiv \textbf{g}_{\rm{eff}}. \]

Our second constraint is for the star to be in thermal balance:

\[ \frac{d\mathcal{L}_{r}}{dr} = 4\pi r^2 \rho \epsilon \]

leading to

\[ \nabla \cdot \mathcal{F} = \rho \epsilon \]

where \(\mathcal{F}\) now depends on \(\Phi_{\rm{eff}}\).

The final result is that for all of these constraints to be true,

Definition 115

\[ \epsilon \propto \left [ 1 - \frac{\Omega^2}{2 \pi G \rho} \right ] \]

Some problems with this:

  • problem is overconstrained

  • energy generation rate cannot be directly proportional to rotate rate - unphysical

Solutions to the von Zeipel’s Paradox#

Something must give. We mush relax some constraints:

  • meridional circulation (Eddington-Sweet Circulation. ) takes part in heat transfer

  • rotation is more complex, possibly depending on \(\bar{\omega}\) and \(z\).

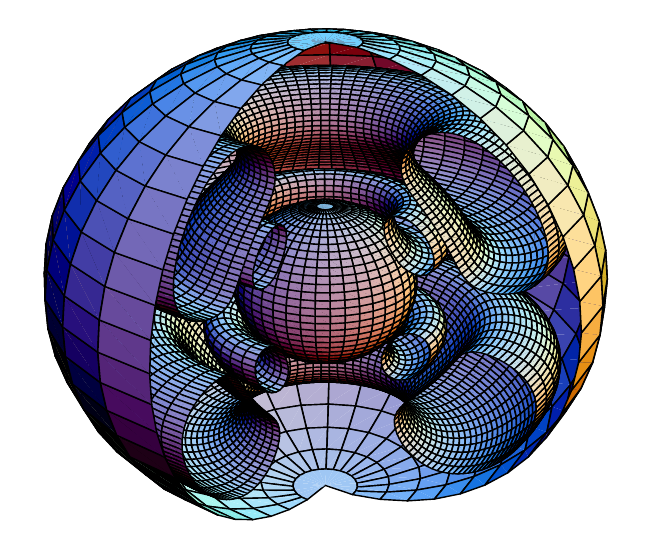
../../_images/es_maeder.png

A schematic illustration of circulation in a 20 solar mass star with an initial rotational velocity of 300 km/s. From Meynet & Maeder 2002. Credit: Astrobites - The consequences of stellar rotation by Nathan Sanders.

The Impact of Rotation of Stellar Evolution#

Helioseismology#

Helioseismology measurements have led to a few observations about our own Sun:

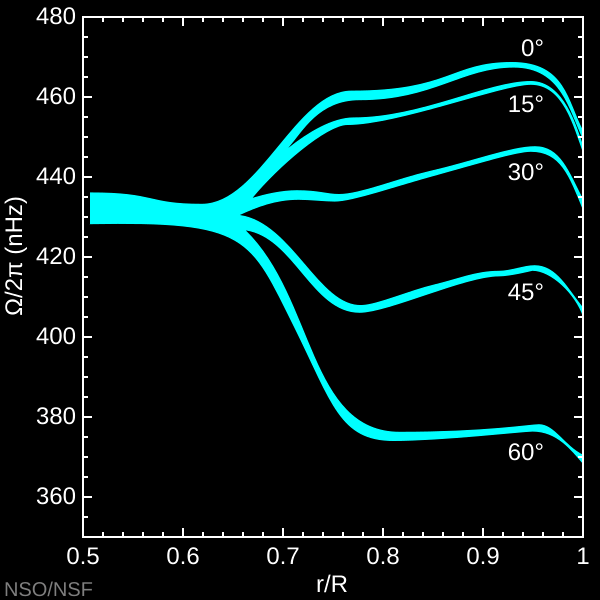
../../_images/tacholine.png

Caption: Internal rotation in the Sun, showing differential rotation in the outer convective region (as a function of latitude) and almost uniform rotation in the central radiative region. The transition between these regions is called the tachocline. Credit: Global Oscillation Network Group.

  1. The Sun is rotating differntially in the outer convection zone as a function of latitude.

  2. The Sun is rotating close to uniform / solid body in the radiative core.

  3. Magnetic fields can help reinforce the strong shear (adjacent layers of fluid moving parallel to each other with different speeds).

Rotation Induced Effects#

  • Extra mixing, leading enhancement (or destruction) of various elements, bringing material from the core to the surface.

  • Extra mass loss, magnetic braking, compact remnant spin rates

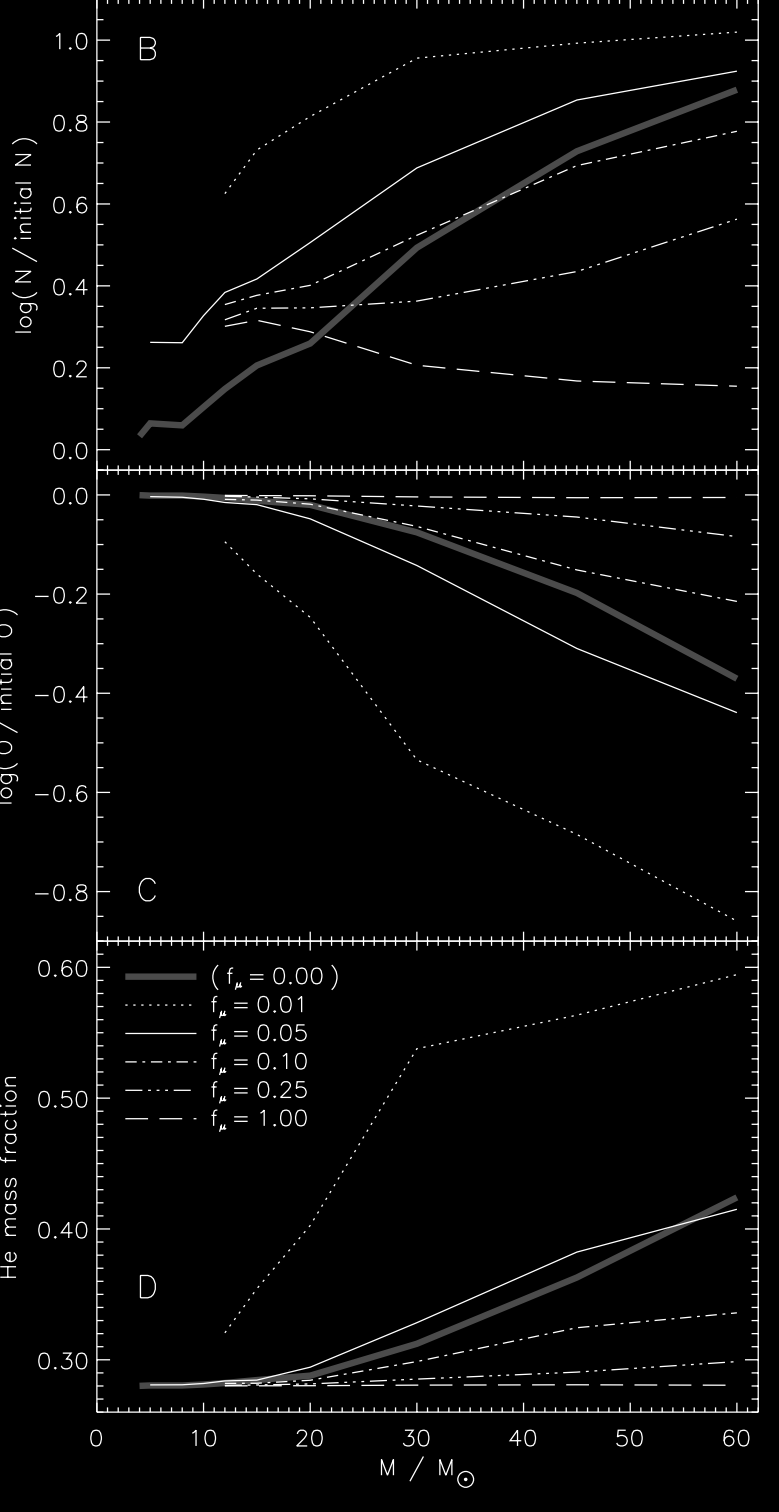
../../_images/nitrogen.png

Surface abundances at core hydrogen exhaustion as function of the initial stellar mass for models with an equatorial surface rotation rate of 200 km / s at ZAMS. From Heger et al 2000.

In-Class Assignment 15#

In-Class Assignment 15 can be found here.

Contents